【理論】平成26年　問9｜複数のLC直列共振回路の接続による共振周波数の変化に関する計算問題

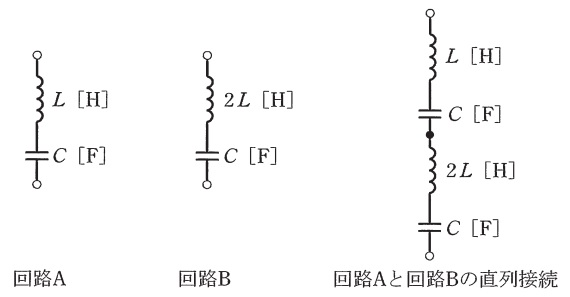
図のように，二つの \( LC \) 直列共振回路 \( \mathrm{A} \)，\( \mathrm{B} \) があり，それぞれの共振周波数が \( f_{\mathrm{A}} \) [Hz]，\( f_{\mathrm{B}} \) [Hz] である。

これら \( \mathrm{A} \)，\( \mathrm{B} \) をさらに直列に接続した場合，全体としての共振周波数が \( f_{\mathrm{AB}} \) [Hz] になった。

\( f_{\mathrm{A}} \)，\( f_{\mathrm{B}} \)，\( f_{\mathrm{AB}} \) の大小関係として，正しいものを次の (1)～(5) のうちから一つ選べ。

回路図

(1)　\( f_{\mathrm{A}} < f_{\mathrm{B}} < f_{\mathrm{AB}} \)
(2)　\( f_{\mathrm{A}} < f_{\mathrm{AB}} < f_{\mathrm{B}} \)
(3)　\( f_{\mathrm{AB}} < f_{\mathrm{A}} < f_{\mathrm{B}} \)
(4)　\( f_{\mathrm{AB}} < f_{\mathrm{B}} < f_{\mathrm{A}} \)
(5)　\( f_{\mathrm{B}} < f_{\mathrm{AB}} < f_{\mathrm{A}} \)

合格への方程式

共振回路の基本原理

共振とは

共振とは、交流回路において電圧と電流が同位相になる状態のことです。この状態では、回路の性質に応じて「リアクタンスが0」または「サセプタンスが0」となります。身近な例えでは、ブランコを押すタイミングと同じで、エネルギーの伝達が最も効率よく行われる状態と考えられます。

共振回路は、コイル（L）とコンデンサ（C）という2つの異なるエネルギー貯蔵素子で構成されます。コイルは電流によって磁界のエネルギーを蓄え、コンデンサは電圧によって電界のエネルギーを蓄えます。

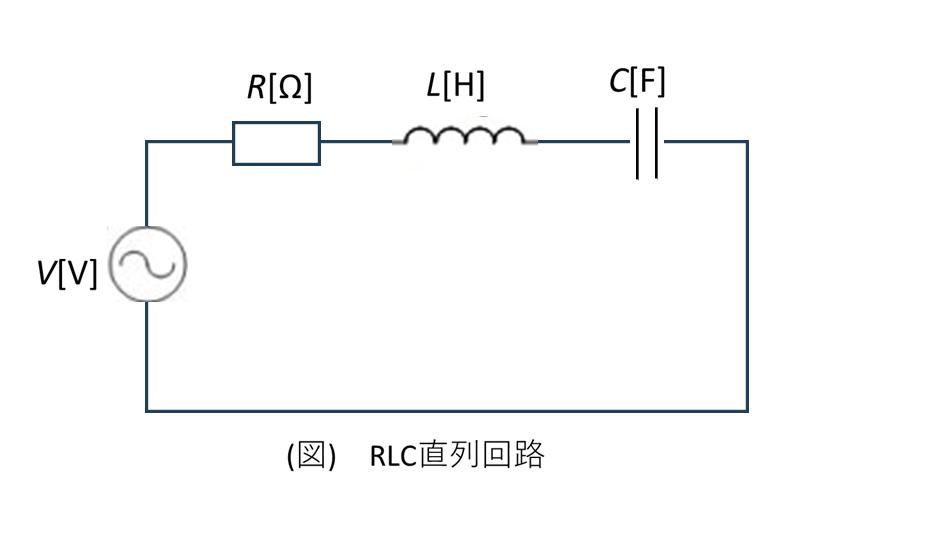
RLC直列回路

図1: RLC直列回路

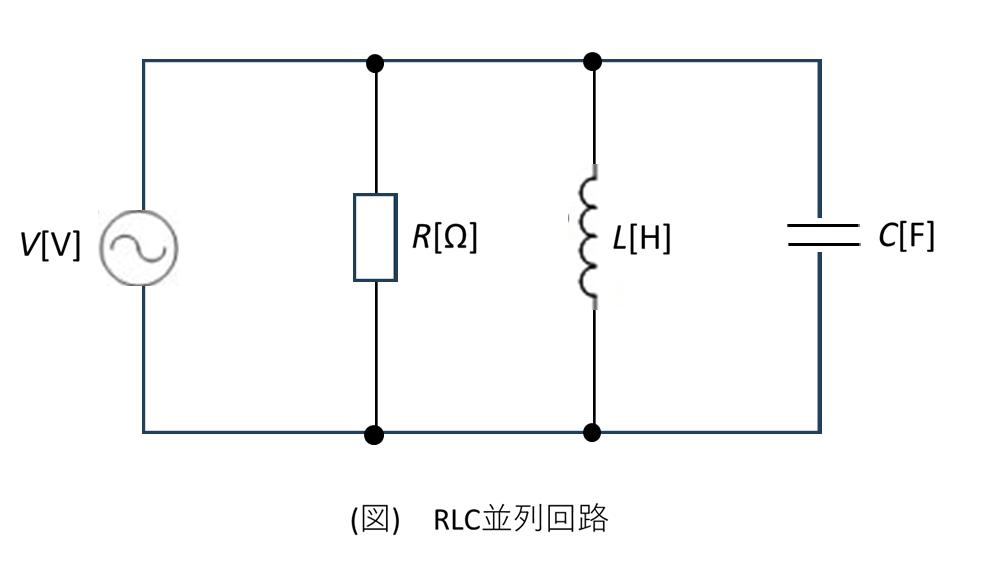
RLC並列回路

図2: RLC並列回路

共振の種類

共振回路には大きく分けて2種類あります：

  • 直列共振回路：LとCが直列に接続され、インピーダンスが最小になる状態
  • 並列共振回路：LとCが並列に接続され、アドミタンスが最小（インピーダンスが最大）になる状態

共振の応用

共振回路は、ラジオやテレビのチューナー、無線通信機器など、特定の周波数を選択する回路として広く利用されています。

直列共振回路

RLC直列回路

直列共振回路の定義

図1のようなRLC直列回路があった場合、特定の周波数（共振周波数）において回路のインピーダンスが最小になる状態を共振と呼びます。

直列共振回路では、コイルとコンデンサのリアクタンスが大きさは同じで符号が反対になるため、互いに打ち消し合います。これにより、回路のインピーダンスは純抵抗性（抵抗Rの値）となります。

直列回路の合成インピーダンス

図1のようなRLC直列回路があった場合の合成インピーダンス Z̄ [Ω] は、角周波数を ω [rad/s] とすると、

→　横スクロールして下さい　→

\[ \begin{aligned} \dot{Z} &= R + \mathrm{j}\omega L + \frac{1}{\mathrm{j}\omega C} \\[10pt] &= R + \mathrm{j}\left(\omega L - \frac{1}{\omega C}\right) \end{aligned} \]

となり、インピーダンスが最も小さくなるためには、上式の虚数部が零である必要があります。よって、共振角周波数 ωc [rad/s] は、

→　横スクロールして下さい　→

\[ \begin{aligned} \omega_{\mathrm{c}} L - \frac{1}{\omega_{\mathrm{c}} C} &= 0 \\[10pt] \omega_{\mathrm{c}} L &= \frac{1}{\omega_{\mathrm{c}} C} \\[10pt] \omega_{\mathrm{c}}^2 &= \frac{1}{LC} \\[10pt] \omega_{\mathrm{c}} &= \frac{1}{\sqrt{LC}} \end{aligned} \]

となります。また、共振周波数を fc [Hz] とすると、ωc = 2πfc より、

\[ f_{\mathrm{c}} = \frac{1}{2\pi\sqrt{LC}} \]

となります。

直列共振回路の特性

  • 共振状態では、回路のインピーダンスが最小（純抵抗R）になります
  • 電流が最大になります
  • コイルとコンデンサの端子電圧は、印加電圧よりも大きくなることがあります
  • 回路全体のリアクタンスが0になります

並列共振回路

RLC並列回路

並列共振回路の定義

図2のようなRLC並列回路があった場合、特定の周波数（共振周波数）において回路のアドミタンスが最小（インピーダンスが最大）になる状態を共振と呼びます。

並列共振回路では、コイル回路とコンデンサ回路を流れる電流は大きさが同じで向きが逆になるため、互いに打ち消し合います。これにより、回路のアドミタンスは最小となります。

並列回路の合成アドミタンス

図2のようなRLC並列回路があった場合の合成アドミタンス Ȳ [S] は、角周波数を ω [rad/s] とすると、

\[ \begin{aligned} \dot{Y} &= \frac{1}{R} + \mathrm{j}\omega C + \frac{1}{\mathrm{j}\omega L} \\[10pt] &= \frac{1}{R} + \mathrm{j}\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]

となり、アドミタンスが最も小さくなるためには、上式の虚数部が零である必要があります。よって、共振角周波数 ωc [rad/s] は、

\[ \begin{aligned} \omega_{\mathrm{c}} C - \frac{1}{\omega_{\mathrm{c}} L} &= 0 \\[10pt] \omega_{\mathrm{c}} C &= \frac{1}{\omega_{\mathrm{c}} L} \\[10pt] \omega_{\mathrm{c}}^2 &= \frac{1}{LC} \\[10pt] \omega_{\mathrm{c}} &= \frac{1}{\sqrt{LC}} \end{aligned} \]

となります。また、共振周波数を fc [Hz] とすると、ωc = 2πfc より、

\[ f_{\mathrm{c}} = \frac{1}{2\pi\sqrt{LC}} \]

となります。

並列共振回路の特性

  • 共振状態では、回路のアドミタンスが最小（インピーダンスが最大）になります
  • 電源から流れる電流が最小になります
  • 内部循環電流（LとC間を流れる電流）は、電源電流よりも大きくなることがあります
  • 回路全体のサセプタンスが0になります

計算例題

例題1: 直列共振回路の共振周波数

インダクタンス L = 4 mH、キャパシタンス C = 4 × 10⁻⁷ F の直列回路の共振周波数を求めよ。

解答

直列共振回路の共振周波数の式は：

\[ f = \frac{1}{2\pi\sqrt{LC}} \]

値を代入すると：

\[ \begin{aligned} f &= \frac{1}{2\pi\sqrt{4 \times 10^{-3} \times 4 \times 10^{-7}}} \\[10pt] &= \frac{1}{2\pi\sqrt{16 \times 10^{-10}}} \\[10pt] &= \frac{1}{2\pi \times 4 \times 10^{-5}} \\[10pt] &= \frac{10^5}{8\pi} \\[10pt] &\approx 3979 \mathrm{\ Hz} \approx 4 \mathrm{\ kHz} \end{aligned} \]

よって、共振周波数は約 4 kHz です。

例題2: 並列共振回路のキャパシタンス

共振周波数が 1 kHz で、インダクタンス L = 0.25 H の並列回路のキャパシタンス C を求めよ。

解答

並列共振回路の共振周波数の式は：

\[ f = \frac{1}{2\pi\sqrt{LC}} \]

この式を C について解くと：

\[ \begin{aligned} C &= \frac{1}{(2\pi f)^2 L} \\[10pt] &= \frac{1}{(2\pi \times 10^3)^2 \times 0.25} \\[10pt] &= \frac{1}{(2\pi \times 10^3)^2 \times 0.25} \\[10pt] &= \frac{4}{(2\pi \times 10^3)^2} \\[10pt] &= \frac{4}{4\pi^2 \times 10^6} \\[10pt] &= \frac{1}{\pi^2 \times 10^6} \\[10pt] &\approx 1.01 \times 10^{-7} \mathrm{\ F} \approx 0.1 \mathrm{\ μF} \end{aligned} \]

よって、必要なキャパシタンスは約 0.1 μF です。

計算時の注意点

共振周波数の計算では、単位を揃えることが重要です。特に：

  • インダクタンス L は通常 H（ヘンリー）単位
  • キャパシタンス C は通常 F（ファラド）単位
  • 周波数 f は Hz（ヘルツ）単位
  • 角周波数 ω は rad/s 単位

また、mH や μF などの単位を使う場合は、計算時に基本単位（H, F）に変換しましょう。

🔍 ワンポイントアドバイス： 直列共振と並列共振の共振周波数の公式は同じ形（f = 1/(2π√LC)）ですが、回路特性は逆になります。直列共振ではインピーダンスが最小（電流最大）、並列共振ではインピーダンスが最大（電流最小）になることを覚えておきましょう。覚え方としては「直列＝電流直進（最大）」、「並列＝電流阻止（最小）」というイメージが役立ちます。

今日は直列共振回路の組み合わせについて勉強していこか！図を見てくれるかな。二つの\(LC\)直列共振回路A、Bがあって、それぞれの共振周波数が\(f_A\)、\(f_B\)やな。そして、これらを直列に接続したときの共振周波数が\(f_{AB}\)になるんや。まず、直列共振回路の共振周波数の基本式を思い出してみようか？

はい、直列共振回路の共振周波数の基本式を確認します。

直列\(LC\)回路の共振周波数\(f_c\)は次の式で表されます：

\( f_c = \frac{1}{2\pi\sqrt{LC}} \)

これは、共振状態でインダクタンスとキャパシタンスのリアクタンスが等しくなる条件から導かれる式ですね。

その通りや！基本式はしっかり覚えとるな。じゃあ次に、回路Aと回路Bの具体的な構成を見てみよか。図から読み取れる情報を整理してくれるかな？回路Aはどんな構成で、回路Bはどんな構成になっとる？

図を見ると、回路の構成は次のようになっています：

回路A：インダクタンス\(L\) [H]とキャパシタンス\(C\) [F]が直列接続

回路B：インダクタンス\(2L\) [H]とキャパシタンス\(C\) [F]が直列接続

つまり、回路Bは回路Aと比べてインダクタンスが2倍になっているのが特徴ですね。

ええ観察力やな！その通りや。回路Aは\(L\)と\(C\)、回路Bは\(2L\)と\(C\)の組み合わせやな。じゃあ、まずは回路Aの共振周波数\(f_A\)を求めてみようか。

回路Aの共振周波数\(f_A\)を求めます。

回路Aは\(L\) [H]と\(C\) [F]の直列接続なので、基本式に代入すると：

\( f_A = \frac{1}{2\pi\sqrt{L \cdot C}} = \frac{1}{2\pi\sqrt{LC}} \)

これが回路Aの共振周波数となります。

完璧や！次は回路Bの共振周波数\(f_B\)を求めてみようか。回路Bはインダクタンスが\(2L\)になっとるから、どう計算するかな？

回路Bの共振周波数\(f_B\)を求めます。

回路Bは\(2L\) [H]と\(C\) [F]の直列接続なので、基本式に代入すると：

\( f_B = \frac{1}{2\pi\sqrt{2L \cdot C}} = \frac{1}{2\pi\sqrt{2LC}} \)

これをさらに変形すると：

\( f_B = \frac{1}{2\sqrt{2}\pi\sqrt{LC}} \)

数値的には、\(\sqrt{2} \approx 1.414\)なので：

\( f_B \approx \frac{1}{2.83\pi\sqrt{LC}} \)

よう計算できとるな！ここで\(f_A\)と\(f_B\)の大小関係を確認してみようか。\(f_A = \frac{1}{2\pi\sqrt{LC}}\)と\(f_B = \frac{1}{2\sqrt{2}\pi\sqrt{LC}}\)を比べると、どっちが大きいかな？

\(f_A\)と\(f_B\)の大小関係を比較します。

\( f_A = \frac{1}{2\pi\sqrt{LC}} \)

\( f_B = \frac{1}{2\sqrt{2}\pi\sqrt{LC}} \)

分母を比較すると、\(2\sqrt{2} > 2\)（\(\sqrt{2} > 1\)のため）です。

分母が大きいほど分数の値は小さくなるので：

\( f_B < f_A \)

つまり、インダクタンスが大きくなると共振周波数は小さくなることが分かります。

ナイス！その通りや。インダクタンスが大きくなると共振周波数は小さくなるんやな。さあ、いよいよ本題や！回路Aと回路Bを直列に接続したときの合成回路について考えてみよか。直列接続したときのインダクタンスとキャパシタンスはどうなるかな？

回路Aと回路Bを直列に接続した場合の合成値を求めます。

直列接続の場合：

合成インダクタンス：\(L + 2L = 3L\) [H]

合成キャパシタンス：コンデンサの直列接続なので

\[ \frac{1}{C_{合成}} = \frac{1}{C} + \frac{1}{C} = \frac{2}{C} \]

したがって、\(C_{合成} = \frac{C}{2}\) [F]

つまり、全体として\(3L\) [H]と\(\frac{C}{2}\) [F]の直列回路になります。

完璧や！合成インダクタンスが\(3L\)、合成キャパシタンスが\(\frac{C}{2}\)やな。じゃあ、この合成回路の共振周波数\(f_{AB}\)を計算してみようか。

合成回路の共振周波数\(f_{AB}\)を求めます。

合成インダクタンス\(3L\) [H]、合成キャパシタンス\(\frac{C}{2}\) [F]を基本式に代入します：

\[ \begin{aligned} f_{AB} &= \frac{1}{2\pi\sqrt{3L \cdot \frac{C}{2}}} \\[10pt] &= \frac{1}{2\pi\sqrt{\frac{3LC}{2}}} \end{aligned} \]

ええ調子や！計算を続けて、分かりやすい形にしてみようか。\(\sqrt{\frac{3LC}{2}}\)をもう少し整理してくれるかな？

式をさらに整理します：

\[ \begin{aligned} f_{AB} &= \frac{1}{2\pi\sqrt{\frac{3LC}{2}}} \\[10pt] &= \frac{1}{2\pi\sqrt{\frac{3}{2}} \cdot \sqrt{LC}} \\[10pt] &= \frac{1}{2\sqrt{\frac{3}{2}}\pi\sqrt{LC}} \end{aligned} \]

ここで、\(\sqrt{\frac{3}{2}} = \sqrt{1.5} \approx 1.225\)なので：

\( f_{AB} \approx \frac{1}{2.45\pi\sqrt{LC}} \)

素晴らしい計算やな！これで3つの共振周波数が全部求まったで。まとめると：

\(f_A = \frac{1}{2\pi\sqrt{LC}} \approx \frac{1}{2.00\pi\sqrt{LC}}\)

\(f_B = \frac{1}{2\sqrt{2}\pi\sqrt{LC}} \approx \frac{1}{2.83\pi\sqrt{LC}}\)

\(f_{AB} = \frac{1}{2\sqrt{\frac{3}{2}}\pi\sqrt{LC}} \approx \frac{1}{2.45\pi\sqrt{LC}}\)

分母の大きさを比較して、大小関係を決めてくれるかな？

3つの共振周波数の大小関係を求めます。

分母の大きさを比較すると：

2.00 < 2.45 < 2.83

分母が大きいほど分数の値は小さくなるので：

\( f_B < f_{AB} < f_A \)

これは選択肢の(5) \(f_B < f_{AB} < f_A\) と一致します。

したがって、正解は選択肢の(5)です。

完璧や！正解は(5)やな！

この問題のポイントをまとめると、直列接続したときはインダクタンスは足し算、キャパシタンスは逆数の和の逆数になることと、共振周波数は\(\frac{1}{\sqrt{LC}}\)に比例するから、\(LC\)の積が大きくなると共振周波数は小さくなるっていうことやな。よう理解できたやろ？

ありがとうございます！この問題を通して、直列共振回路の合成について理解が深まりました。

重要なポイントをまとめると：

1. 直列接続では、インダクタンスは単純に加算される

2. 直列接続では、キャパシタンスは\(\frac{1}{C_{合成}} = \frac{1}{C_1} + \frac{1}{C_2}\)の関係になる

3. 共振周波数は\(f = \frac{1}{2\pi\sqrt{LC}}\)で決まるため、\(LC\)の積が大きくなると周波数は小さくなる

4. 今回の場合、\(f_B < f_{AB} < f_A\)の関係となり、答えは選択肢の(5)になります。

解説まとめ

■ LC直列共振回路の特性とは

LC直列共振回路は、インダクタンスLとキャパシタンスCが直列に接続された回路です。特定の周波数において、誘導性リアクタンスと容量性リアクタンスが等しくなり、両者が打ち消し合って回路のインピーダンスが最小になる現象を共振といいます。共振周波数は回路のL・C値によって決まり、複数の回路を組み合わせた場合の共振周波数は、各素子の合成値によって決定されます。

■ 計算手順と公式

  1. LC直列共振回路の共振周波数

    LC直列回路の共振周波数は次式で求められます。

    \( f = \frac{1}{2\pi\sqrt{LC}} \)

    ここで、fは共振周波数[Hz]、Lはインダクタンス[H]、Cはキャパシタンス[F]です。

  2. インダクタンスの直列合成

    インダクタンスを直列接続した場合の合成インダクタンスは単純な和になります。

    \( L_{total} = L_1 + L_2 + \cdots + L_n \)

  3. キャパシタンスの直列合成

    キャパシタンスを直列接続した場合の合成キャパシタンスは逆数の和の逆数になります。

    \( \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n} \)

    同じ容量C のコンデンサ2個を直列接続した場合: \( C_{total} = \frac{C}{2} \)

  4. 複数回路の直列接続時の共振周波数計算

    各回路の素子値を合成し、新たなL・C値から共振周波数を計算します。

■ 具体的な計算例

問題条件

  • 回路A: インダクタンス2L、キャパシタンスC
  • 回路B: インダクタンスL、キャパシタンスC
  • 回路ABは回路AとBを直列接続

回路Aの共振周波数の計算

\[ \begin{aligned} f_A &= \frac{1}{2\pi\sqrt{LC}} \end{aligned} \]

回路Bの共振周波数の計算

\[ \begin{aligned} f_B &= \frac{1}{2\pi\sqrt{2LC}} \\[5pt] &= \frac{1}{2\sqrt{2}\pi\sqrt{LC}} \\[5pt] &\approx \frac{1}{2.83\pi\sqrt{LC}} \end{aligned} \]

回路A・Bを直列接続した場合の合成値

合成インダクタンス:

\[ \begin{aligned} L_{AB} &= 2L + L = 3L \ \mathrm{[H]} \end{aligned} \]

合成キャパシタンス:

\[ \begin{aligned} C_{AB} &= \frac{C \cdot C}{C + C} = \frac{C}{2} \ \mathrm{[F]} \end{aligned} \]

回路ABの共振周波数の計算

\[ \begin{aligned} f_{AB} &= \frac{1}{2\pi\sqrt{3L \cdot \frac{C}{2}}} \\[5pt] &= \frac{1}{2\pi\sqrt{\frac{3}{2}LC}} \\[5pt] &= \frac{1}{2\sqrt{\frac{3}{2}}\pi\sqrt{LC}} \\[5pt] &\approx \frac{1}{2.45\pi\sqrt{LC}} \end{aligned} \]

共振周波数の大小関係の比較

各共振周波数の分母を比較すると:

  • \( f_A \): 分母は \( 2\pi\sqrt{LC} \) ≈ \( 2\pi\sqrt{LC} \)
  • \( f_B \): 分母は \( 2.83\pi\sqrt{LC} \)
  • \( f_{AB} \): 分母は \( 2.45\pi\sqrt{LC} \)

分母が大きいほど周波数は小さくなるため:

2 < 2.45 < 2.83 の関係から

結論：\( f_B < f_{AB} < f_A \) となる。（解答：選択肢(5)）

■ 実務上の留意点

LC共振回路の設計と応用における実務上の留意点です。